The Mother (Nature) of All Wars?
Modern Wars, Global Terrorism, and Complexity Science
by Neil F. Johnson
It has become hard for us to watch a nightly news bulletin without hearing phrases such as “thirty dead in Iraq,” “five wounded in Afghanistan,” “three guerrilla attacks in Colombia,” or “ten killed in a terrorist bomb in Indonesia.” We are then typically presented with a number of studio experts who try to explain away the numbers by drawing on idiosyncratic details of the conflict in question. Although often unconvincing, their approach is perfectly defensible given the very different origins, motivations, locations and durations of these separate conflicts. However recent research by a multi-disciplinary team of Complexity scientists suggests that all these sociological, political and strategic experts may have missed something crucial.
Using techniques from the physics of Complex Systems, the research team has shown that the dynamics underlying all such modern conflicts, including global terrorism, are remarkably universal. Furthermore they have developed a physics-based theory describing the dynamics of insurgent group formation and attacks, which neatly explains the universal patterns observed in all modern wars and terrorism. The implications are quite sobering: Regardless of the origins and locations of modern conflicts, the insurgent groups in each case are operating in the same way. In short, it is effectively the same enemy on all fronts.
There are two reasons why the field of human conflict should be of interest to a physicist. First, the increased availability of computerized datasets means that there is a data revolution underway across the social sciences–just as the field of astronomy recently caught alight as a result of improved data collection. Human conflict is as old as mankind itself–however, a lack of reliable time-series data in the past has kept it out of reach of the quantitative sciences. This has now changed with the media, governments and non-governmental organizations all now regularly collecting data on ongoing conflicts. Admittedly the analysis of their datasets is not always straightforward–not only do the individual agencies differ in their numbers, but the way in which the figures are reported can differ quite markedly. Extensive cross-checks from the various sources must therefore be carried out prior to any data analysis.
The second reason touches the fascinating aspect of Complexity Science itself. In particular, modern wars seem to exhibit all the common characteristics of Complex Systems: (1) There is feedback, both at the microscopic and macroscopic scale, yielding a system with memory and non-Markovian dynamics. (2) The time-series of events is non-stationary. (3) There are many types of “particle,” according to the various armed actors, and they interact in possibly time-dependent ways. The war's evolution is then driven by this ecology of agents. (4) The agents can adapt their behavior and decisions based on past outcomes. The system is far from equilibrium and can exhibit extreme behavior–for example, if the strategies of several groups of agents suddenly coincide. (5) The observed war constitutes a single realization of the system's possible trajectories. (6) The system is open, with this coupling to the environment making it hard to distinguish between exogenous (i.e. outside) and endogenous (i.e. internal, self-generated) effects.
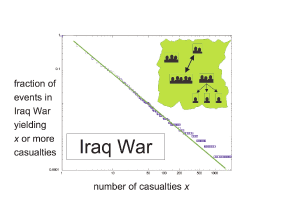 |
Mike Spagat from the University of London, Jorge Restrepo and Roberto Zarama in Bogota, Colombia, and I have compiled, cross-checked and analyzed event datasets for a wide variety of ongoing and recent wars, including acts of global terrorism. In each case, we plotted the histogram of the number of events within a given war with x or more casualties, versus x, on a log-log plot. What we found was really quite startling. Although wars are the antithesis of a ordered system, the datapoints for each war fell neatly on to a straight line (see the figure). This suggests a power-law behavior, which we then confirmed statistically. We repeated this exercise for wars as diverse as Israel, Senegal, Peru, Afghanistan and Colombia. In each case we obtained a power-law, i.e. the fraction of events with x casualties varies as x-a. This finding is remarkable given the different conditions, locations and durations of these separate wars. For example, the Iraq war is being fought in the desert and cities and is fairly recent, while the twenty-year old Colombian war is being fought in mountainous jungle regions against a back-drop of drug-trafficking and Mafia activity. This power-law finding also has some very important practical implications in terms of military planning. It means there is no typical size of event–unlike the bell-curve for population heights, for example, which is centered around an average height. Deadly events with many casualties will occur–rarely, but they will occur. This is again unlike the case of heights, where the chances that someone will be taller than ten feet are truly negligible.
But the surprises don't stop there. Not only did we obtain straight-line slopes, but these slopes all produced a power-law exponent α near 2.5. Furthermore Aaron Clauset and co-workers recently analyzed an extensive database of global terror events, and also obtained a power-law–with an α value equal to 2.5. By contrast when we looked at data from older wars–such as the civil wars in the US, Spain and Russia –we found no statistical evidence for a power-law at all. Furthermore, the power-law exponent is insensitive to any systematic over- or under-reporting of casualties, because the overall number of casualties is just a normalizing factor. Hence the power-law signature successfully focuses on the war's internal pattern of events and hence casualties, as opposed to simply monitoring the aggregate number.
But why should 2.5 be such a magic number for modern wars and global terrorism? To answer this, we developed a model of dynamical group-formation to describe an insurgent force. Our cue came from the fact that most modern wars, including terrorism, can be characterized by an asymmetric ‘David-and-Goliath’ structure in which a small, but agile, insurgent force faces a much stronger, but more rigid, institutional force such as a state’s army. Because of its less rigid structure, the insurgent force is able to self-organize itself into a loosely connected soup of attack units which combine and dissociate over time in response to their own ad hoc operations, and in response to the state army's operations. These attack units are shown in the inset in the figure. The number of dark shadows in each unit is proportional to the number of casualties that that unit will inflict in a typical conflict event. Each attack unit comprises a group of people, weapons, explosives, machines, or even information, which temporarily organizes itself to act as a single unit. In the case of people, this means that they are probably connected by a common location, or by some common communication system. However, an attack unit may also consist of a combination of people and objects–for example, explosives plus a few people, such as in the case of suicide bombers. Such an attack unit, while only containing a few people, could have a high attack strength. Information could also be a valuable part of an attack unit. A lone suicide bomber who knows when a certain place will be densely populated–for example a military canteen at lunchtimes–and who knows how to get into such a place unnoticed, will also represent an attack unit with a high attack strength. When a given attack unit undertakes an attack, it creates a number of casualties proportional to its strength–hence the distribution of attack-unit strengths will reflect the distribution of casualties which arise in the war.
When our model is solved analytically, it produces a power-law with α =2.5. If we then make the group formation-dissociation probabilities depend on the existing group sizes, this α value can be moved toward 2.0 or 3.0, thereby incorporating all the results for modern wars. Generalizing the model further to include multiple insurgent groups, yields a near-perfect fit with the real data over the entire range of x, including the nonlinear deviations at high and low x. Hence we can explain the entire range of casualty events in all modern wars and terrorism using slight variations of the same basic model.
While outside the realm of traditional physics, this new line of physics research has led to a novel quantitative understanding of current world conflicts, terrorism and insurgent warfare. In particular, it suggests that the dynamics of insurgent group formation are the same across all arenas–from the jungles of Colombia through to the deserts of Iraq, and including the entire world stage of global terrorism. In short, the way in which modern wars and terrorism are being waged has less to do with geography or ideology, and more to do with the day-to-day mechanics of human insurgency–in other words, it is simply the way in which insurgent groups of human beings fight when faced with a much stronger, but more rigid, opponent. As a consequence of this, it would seem that unless the stronger, but more rigid, opponent can change its tactics, the same statistical patterns of casualties will be repeated indefinitely into the future.
What about the future of this research? Having looked at event sizes, we are now focusing on their timing–not only in ongoing wars, but also in organized crime activity including homicides, kidnappings and extortion. With the help of Sean Gourley, Juan Camilo Bohorquez and Elvira Restrepo at the Universidad de Los Andes in Colombia, we have successfully created multi-agent models which mimic the decision-making dynamics of insurgent groups, just as had been done earlier for groups of financial traders within the so-called Econophysics community (see Financial Market Complexity (Oxford University Press, 2003)). By analyzing the size, timing and spatial coordinates of a given event, as well as the groups involved, we are now able to reconstruct the possible trails which a particular insurgent group might have followed. Just as in a multi-species ecological setting within the natural world, we are interested in determining the behaviors and possible protocols which arise when a particular group from insurgent army A happens to cross the path of a particular group from insurgent army B. In particular, we are trying to deduce whether they decide to fight each other, collaborate, ignore each other–or even consciously avoid each other. Going further, we know that wars like the ones in Colombia and Afghanistan have taken place against the backdrop of an illicit trade such as drug trafficking. This activity provides an effective nutrient supply in the form of money for buying supplies and weapons, and thereby helps feed the war as a whole. So just like a fungus will thrive in a forest, or a cancer tumour will thrive in a host, these armed groups are fed by a rich source of nutrients which allows them to self-organize into a robust structure. Admittedly, just like a jungle itself, this is all very far from our everyday experiences as physicists. But the exciting news is that the tools to help answer such unlikely questions are now beginning to emerge –and they are emerging from a very unlikely source: Physics.
 |
©1995 - 2024, AMERICAN PHYSICAL SOCIETY
APS encourages the redistribution of the materials included in this newspaper provided that attribution to the source is noted and the materials are not truncated or changed.
Contributing Editor: Jennifer Ouellette
Staff Writer: Ernie Tretkoff
November 2006 (Volume 15, Number 10)
Articles in this Issue

