The Back Page

Physicists and Traffic Flow

By Craig Davis

Craig Davis

Most of us have experienced the frustration of traffic congestion on urban freeways. Often, for no apparent reason, traffic will slow to a crawl or even a standstill and after several minutes return to normal speeds. Perhaps this was caused by an earlier incident, but it is seldom evident. Usually a jam will persist until traffic has thinned considerably.

Congestion costs almost 100 billion dollars annually in this country when wasted time and fuel are computed, to say nothing of the increased air pollution and accident rates. The United States is not unique in this phenomenon—most major cities worldwide experience the same problem. Further construction of freeways to alleviate congestion is unlikely in many cities. Thus it is imperative to understand traffic better and to devise methods to use existing capacity more efficiently.

One of the first physicists to study traffic flow was Robert Herman of the General Motors Research Laboratory.

In the 1960s, he and colleagues (which included Ilya Prigogine and Elliott Montroll) applied principles of statistical physics to traffic. Models they developed are still used today in some large-scale commercial simulation codes. One successful outcome of this work was the counter-intuitive suggestion to reduce congestion by installing traffic lights at the entrance to the Lincoln Tunnel.

Interest within the physics community languished until the late 1980s when several developments took place. On the empirical side, good data on traffic flow was obtained using instrumented highways, particularly in Europe.

At the same time, theoretical concepts such as self-organization and simulations based on cellular automata were applied to traffic flow. Although traffic is a dynamical system far from equilibrium, the notion of phase transitions can be used to describe abrupt changes in flow. These transitions are considered first order because hysteresis is observed.

Jamming and Synchronized Flow
The simplest transition is free flow to a jam—referred to as the jamming transition. A traffic jam on a freeway (where vehicles go abruptly from highway speeds to near standstill and later return to their original velocities) is a striking example of self-organized behavior. No person or agency orchestrated this collective action. (We exclude from consideration jams formed by accidents in which the road is blocked.) When the density of vehicles is large enough (~30/km), a random event such as a fluctuation in a leading car's velocity can induce a transition from free flow to the jammed phase. As approaching vehicles slow down, the leading edge of the jam propagates upstream. The speed of propagation is ~15 km/h. The width of the jam grows because more vehicles are added to the jam than leave at the downstream boundary, which propagates at a slower pace.

Once a jam has formed, it persists until the incoming flow drops sufficiently for the width to vanish. Parameters that determine the critical density for jamming include driver reaction times (~1 second) and the mechanical time constants of vehicles.

In multi-lane highways, when traffic density is high enough, lane changing tends to equilibrate vehicle speeds across lanes. This phenomenon is called synchronization. Although synchronization of speed is obvious in the data, the significance of a transition to the synchronized flow phase has only recently been appreciated.

Apparently the sequence of transitions (a) free flow to synchronized flow and then (b) synchronized flow to a jam is more common than simply jamming.

Synchronized flow differs from jamming in several respects. First of all, the reduction in vehicle velocity is not severe. Typical speeds are in the range 20-40 km/h. Flow rates are also larger, although nowhere near the maximum capacity of ~2500 vehicles/h in each lane.

The distinguishing feature of transitions from free flow to synchronized flow is the "bottleneck." It can be as simple as a region of reduced speed (due to road construction, for example) or the termination of a lane.

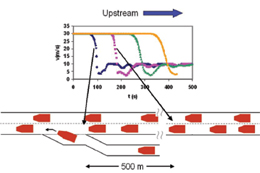Figure 1. Vehicle velocities in synchronized flow (schematic). The blue points are for vehicles passing the onramp. The other colored points are for equal distances upstream, illustrating the propagation of the leading edge of the transition from free flow.

Even vehicles slowing down to exit a freeway can induce synchronized flow. However, synchronized flow typically is induced by onramps. Merging vehicles disrupt the normal flow of the freeway as oncoming vehicles slow or switch lanes to accommodate them. If merging is frequent and the mainline flow is high, the average velocity of oncoming traffic drops in the neighborhood of the onramp. Just as in jamming, the region of reduced speed must propagate upstream because the incoming rate exceeds the flow in the bottleneck. (See Figure 1.) The downstream boundary of reduced velocity is pinned at the bottleneck. The total flow emerging from the bottleneck is limited by the capacity of the remaining freeway lanes.

Highway traffic data clearly indicate the difference between free flow and synchronized flow.

The flow rate is a product of the average velocity and the density. Since the velocity does not vary much with density up to about 20 vehicles/km, the plot of flow against density is nearly linear.

Above that density, however, the average vehicle velocity, and especially the flow rate, drops precipitously. The data no longer fall on a curve but occupy a broad region in flow-density space. (See Figure 2.)

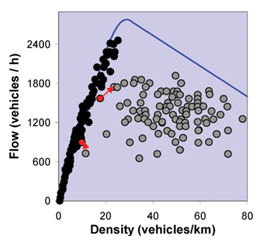Figure 2. Schematic fundamental diagram (solid line) and measured traffic flow on a German autobahn. Vehicle flow is linear with increasing density up to a critical density of ~30 vehicles/km. Above that density, a perturbation can cause a transition to synchronized flow (upper red arrow at ~18 vehicles/km), from which the system does not recover until the density drops to much lower value (lower red arrow at ~11 vehicles/km). (Adapted by Craig Stephan and the author from B. S. Kerner and H. Rehborn, 'Experimental properties of phase transitions in traffic flow', Phys. Rev. Lett. 79, p.4030-33, 1997.)

Models and simulation
There is no shortage of traffic models, although none is entirely satisfactory. A key ingredient in most models is the tendency of drivers to slow down as the density of vehicles increases. This implies that a plot of average flow rate (in the absence of transitions) versus density, the so-called fundamental diagram (See figure 2), increases linearly at low densities, levels off at a characteristic density of ~30 vehicles/km, and then drops to zero as the density approaches bumper-to-bumper conditions. The region of declining flow rate is associated with instability.

Boris Kerner of DaimlerChrysler AG and collaborators have proposed and championed the three-phase traffic model. The three phases are free flow, synchronized flow, and jams. The latter two phases can be further classified according to several subcategories.

Complex patterns of flow that may be a combination of phases are frequently observed. Simulations using the optimistically named "intelligent driver model" of traffic flow suggest other patterns with descriptive names such as triggered stop-and-go waves and oscillatory congested traffic.

Dirk Helbing of the Institute for Economics and Traffic in Dresden, Germany and his associates developed the intelligent driver model. The equilibrium solutions of their model fall on the fundamental diagram curve.

Kerner has challenged this result, common to a number of models. He thinks that equilibrium solutions should occupy a two-dimensional region of flow-density space, not just a curve. Perhaps the most significant consequence of the three-phase model is the questions it raises about the validity of the fundamental diagram. The traffic research community has not yet reached a consensus on this point.

The study of traffic flow and its connections to non-equilibrium statistical physics and modern concepts from complexity theory has now captured the attention of many in the physics community, and their papers in Physical Review Letters and Physical Review E are frequently referred to by prominent traffic engineers.

As gratifying as this is, it will become truly satisfying when our newfound knowledge leads to substantial improvements in traffic flow, the efficient use of freeway capacity, and reduced congestion.

How might this be accomplished? Further investigation of traffic metering, which has been in use for over three decades, might be productive. By restricting the flow of incoming vehicles from onramps, freeway congestion has been reduced but not completely eliminated. Also, traffic information provided to drivers electronically or by roadside signs can help drivers choose alternative routes and avoid troubled areas. Likewise, simulations with dynamic speed limits show promise (assuming compliance).

Some researchers suggest that adaptive cruise control can alleviate congestion. In such systems, which are just now becoming available commercially, vehicle speed is controlled by measuring the range (and its time derivative) to the preceding vehicle. Intelligent vehicle systems with dual-mode vehicles are being discussed for the longer term. Clearly there is room for innovative new ideas in traffic theory and control.

Craig Davis is an adjunct professor in the Physics Department at the University of Michigan. He retired from the Ford Motor Company research labs two years ago.