Pedagogical Energy Modeling
Oil Production
As physicists, most of us would agree with Neils Bohr when he stated there is nothing more difficult to predict than the future. We do not expect to be able to write a set of equations which would allow us to predict with certainty the future petroleum production at a particular price, or the future demand for petroleum. Nevertheless, there is a considerable amount of data available on relevant topics which can be used to speculate about our energy future: the production rates of energy of various types, energy resources, demand for energy by each sector, known and projected economics, environmental impacts (known or projected), the advent of improved technologies and so forth.A good example of predictive success in energy matters is the work of King Hubbert1, who in 1957 predicted U.S. petroleum production would peak between 1966 and 1971. This prediction correctly bracketed the actual peak year of 1970 when the U.S. production for the lower-48 states was 9.1 million barrels per day, or 3.3 billion barrels/year (Gb/y). For a variety of reasons, King Hubbert's model for petroleum production has not been as successful in other situations. However, we would like to discuss the model here as a pedagogical example that uses historical U.S. petroleum production data to show the general effects of a finite resource. Interestingly enough, King Hubbert did not include economics in his model. This simplification was somewhat valid prior to the oil embargo of 1973-74 because the price of oil was relatively constant. Petroleum economics is a social science that depends not only on economic principles, but also on economic parameters that depend on psychological perceptions, current political and military situations, modal shifts to alternative fuels, dependence on demand patterns, improvements in energy efficiency, enhanced petroleum recovery from such as methods as flexible drilling, and so forth.
In many instances population data or the rate of consumption of a new product increases exponentially with time, until events change circumstances and a different curve is followed. U.S. petroleum production follows an exponential curve during the first six decades (1860-1920) after the discovery of oil in Pennsylvania in 1859. In Fig. IV.3.1, we see that the log of the U.S. production closely follows a straight line for these first six decades. This remarkable linearity implies that in this case one can phenomenologically link the rate of production, dQ/dt, to the total amount of petroleum consumed at the time of production, Q, giving dQ/dt = lQ. One can somewhat rationalize this relationship by stating that the U.S. production rates were approximately proportional to the maturity of the petroleum industry when it is represented by the total amount of petroleum produced. When limiting factors arise, one would expect deviations from this simple model. By fitting the data from 1860-1920, we obtain l = 0.09 or a growth rate of 9.0 %/year over those six decades.
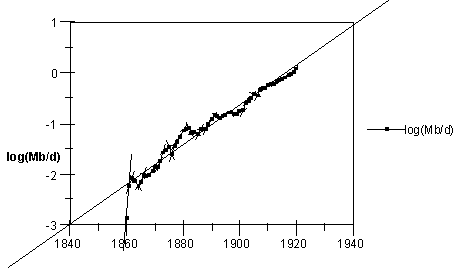
Fig. IV.3.1. Log of U.S. petroleum production rate from the lower-48 states for the years 1860 to 1920, the first 6 decades of production. The data has been fit to an exponential with a growth rate of 9.0 %/year. In 1860, the first full year of production, 500 barrels were produced. (Data obtained from the Energy Information Agency.)
Since petroleum supplies at a fixed cost are finite, it is clear that the unbounded exponential relation can not predict petroleum production in later years. King Hubbert 1 modified the rate equation by defining the finite the petroleum supply available at a given cost as Q o and by requiring that the production rate be proportional to the fraction of the unused resource (1 - Q/Qo). Thus, when the resource has been depleted (Q = Qo), production stops. The resulting equation is familiar to physicists as the Verhulst equation with solutions that look somewhat like Gaussian or Lorentizian curves with symmetrical production rates centered around the year of maximum pumping:
dQ/dt = (lQ/Qo)(Qo - Q) = kQ(Qo - Q).
where k = l/Qo. In Fig. IV.3.2, the U.S. oil production from the lower-48 states from the years 1890 to 1995 is reasonably symmetrical around the year 1970. It is generally predicted that the right shoulder of the curve for the years after 1980 will not fall symmetrically, but will remain relatively constant at about the present reduced rate. The accompanying Verhulst curve fits the data reasonably well, but is expected to fail in the later years. The parameter Qo was obtained2 from the maximum production rate,
d(dQ/dt)/dQ = 0 = k(Qo - 2 Qm),
where Qm is the amount of produced resource when dQ/dt is a maximum. Since one half of the production has taken place at that point, Qm is Qo/2.
Thus, dQ/dtm = kQm(Qo - Qm) = kQo2/4. From the maximum production rate of 3.28 Gb/y, we obtain Qo = 150 G barrels which is fairly close to King Hubbert's 1969 value1 of 165 Gb. Using the value for Qo = 150 Gb and g = kQo = 0.090 from Fig. IV.3.1, we obtained the curve in Fig. IV.3.2. The area of the curve represents the complete reserve Qo and it can be represented to within 6% by2 the product of the maximum pumping rate, dQ/dtm, and G, the full width at half-maximum. Using this we obtain,
G = Qo/(dQ/dtm) = Qo/(kQo2/4) = 4/kQo = 4/l .
From this we obtain G = 4/l = 4/0.09 = 44 years, which is very close to King Hubbert's value of 45 years.
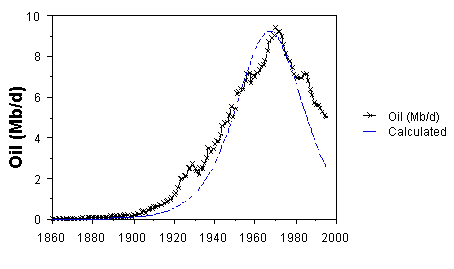
Fig. IV.3.2. U.S. oil production data (x) from the lower-48 states from its beginning in 1860 to the present, 1995. The curve was calculated using Qo = 150 Gb and l = 0.090. It is widely expected that future production will not maintain the symmetry of past production, but rather it is expected that higher prices will maintain production at a level somewhat similar to today's production rate. (Data from EIA.)
Higher petroleum prices will increase the recoverable resource Qo by allowing the use of higher-cost resources and by the use of higher-cost petroleum recovery methods. In addition, higher petroleum prices will reduce petroleum demand. It is generally agreed that relatively small increases in the price will have a small effect since the demand elasticity and the price rise are both small. However, with price rises of several dollars/gallon, the net effect would be quite large since the demand elasticity increases considerably and the price rise is large. We have taken into account2> these these effects by using supply and demand elasticities functions and petroleum pricing functions, but the results are too speculative to describe here. The Department of Energy considered these economic factors and resource data bases in their estimates in Fig. IV.3.3 below.
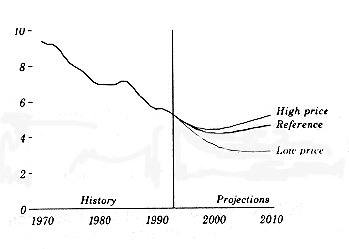
Fig. IV.3.3. Department of Energy forecasts for production from the Lower-48 States as a function of pricing level. (Annual Energy Outlook, DOE, 1995, p. 40)
Energy Usage
Before the oil embargo of 1973-74, U.S. energy use increased by about 4.2%/y during the decade 1960-70. In 1973, the year the oil embargo began, U.S. energy consumption had a relative peak of 74.3 quads. Mostly because of conservation measures, energy use dropped to 70.5 quads in 1983. However, longer term energy trends raised it to 74.3 quads in 1986, about the 1973 level. In more recent years, energy use has risen to 88.5 quads in 1994.The ratio of energy consumption per dollar of gross domestic product is a useful way to consider gross energy usage because, to first order, it removes the twin factors of economic and population growth. This ratio is only part of the energy story because it includes both increases in end-use efficiency as well as modal shifts between different industries. For example, replacing steel mills with computer soft-ware offices saves energy and still raises the GDP. For many years this ratio was considered fixed, a lock-step relation between the economy and energy usage. For the first decade or so after the oil embargo, this ratio decreased from 19,000 BTU/$ in 1973 to 12,900 BTU/$ in 1995 (1992 dollars). A good fraction of this reduction in energy usage per dollar was obtained from increased end-use efficiency, particularly from more energy efficient automobiles, appliances and buildings, with the reamaining shift caused by shifts within the economy.
It is beyond the scope of this paper to predict future energy growth patterns, but it will be pedagogically useful to consider some basic elements which affect energy usage, such as the gross domestic product (GDP), the "efficiency" of turning energy into money (h = GDP/E), and the productvity of a laborer (P = GDP/L). As a beginning, U.S. energy consumption rate (E) can be expressed as:
E = GDP/h = P L/h.
The "efficiency" e takes into account both enhanced end-use efficiency and modal shifts within the economy. By taking the differential of this equation, we obtain:
DE/E = DGDP/GDP - Dh/h = DP/P + DL/L - Dh/h
In the years since the oil embargo, the GDP has been growing at about 2.7%/year (in constant dollars) and U.S. population increases at about 1% per year. The 2.7% growth rate in GDP was caused on average by a 1% growth rate in the population and a 1.7% growth rate in productivity. If we consider the time frame when energy consumption at the end points remained constant (1973-1986), the 2.7%/year in GDP was accomplished with an improved efficiency (real efficiency plus modal changes) of 2.7%/year. This is not surprising because the U.S. has been a wealthy nation with abundant energy supplies, and therefore was less concerned about using energy efficiently. However, during the decade of 1984-94, energy growth rose by 1.8%/year. During this decade, the improvement in "efficiency" dropped to 0.9%/year (1.8 = 2.7 - 0.9). The Department of Energy speculates a continuing increase in "efficiency" in the fuiture of about 1% per year, which just about balances the 1% annual growth in population. If the GDP were then to grow at 2.5%/year, energy usage would rise at 1.5%/year. On the other hand, further enhanced energy efficiency in buildings, transportation and industry can reduce these energy demands.
References
- M. King Hubbert, "Energy Resources," Resources and Man, Nat. Acad. Science, Freeman, San Francisco, 1969, http://ganesa.com/ecotopia/hubbert.html.
- D. Hafemeister, Am. J. Phys. 50, 29-38 (1982).
