Physics and Technology Forefronts

Magnetorheological Materials 

By John M. Ginder

Magnetorheological (MR) materials comprise magnetizable particles dispersed in a nonmagnetic host. In MR fluids, the particles are usually micrometer-sized carbonyl iron powders in a host medium such as natural or synthetic oil; in magnetic powders, the fluid medium is air. These materials transform from freely flowing to weakly solid under an applied magnetic field, a dramatic phenomenon that is the basis for a variety of commercial applications of these controllable or 'smart' materials. In MR elastomers, the particles are locked into viscoelastic solids, but these composites exhibit substantial magnetostriction. While MR fluids are similar to ferrofluids, nanometer-sized colloidal dispersions of single-domain magnetic particles, the two materials possess rather different behaviors: ferrofluids display only small increases in viscosity with field, unlike MR fluids, because the magnetic forces in ferrofluids are orders of magnitude smaller.

Background

The development of MR applications has had an intriguing and instructive history, undergoing several cycles of scientific discovery, technological 'hype,' waning interest, rediscovery and, finally, commercial utilization in the late 1990s.

Developments in MR materials have often paralleled those in electrorheological (ER) fluids, dispersions of electrically polarizable particles that exhibit field-induced solidification under high electric fields. These were extensively investigated by Willis Winslow in his basement laboratory in the 1930s.

Winslow inspired Jacob Rabinow of the National Bureau of Standards to develop their magnetic analogs in the late 1940s, demonstrating proofs-of-concept for many MR devices that would finally become feasible to produce and use five decades later, enabled by developments in chemistry, physics, materials science, and mechanical and electrical engineering.

The remarkable field-induced changes in MR materials are driven by dipolar magnetic attractive forces which form "pearl chains" of particles aligned with the field. These chains store magnetostatic energy and resist mechanical deformations that would reduce the energy. Particle chaining is relevant in a remarkable variety of systems, from magnetic toys and animated displays to natural "compasses" formed from nanoscale ferrite particles in magnetotactic bacteria. While real structures are often complicated due to the broad particle size distribution and high volume fraction f in practical MR materials, our understanding of magnetorheology has been greatly enhanced by studying particle chains.

Magnetic Forces

Much of the scientific research in magnetorheology has focused on quantifying the interparticle magnetic interactions, understanding the dynamics of structure formation, and characterizing the resulting field-induced mechanical properties.

While the interparticle magnetic interactions are approximately dipolar, multipole and many-particle effects, as well as magnetic nonlinearity and saturation, are important. Analytical solutions that account for nonlinearity and saturation are difficult, so my coworkers and I used a finite-element numerical approach to solve for the spatial variation of the magnetic field H and flux density B in a uniform chain of magnetically saturable particles.

Figure 1: Left: electron micrograph of particle chains formed by solidifying carbonyl iron particles in a natural rubber matrix in a flux density of 5kG. Right: spatial variation of magnetic flux density (color contours) and flux lines (lines) in an idealized particle chain as obtained by finite-element analysis.

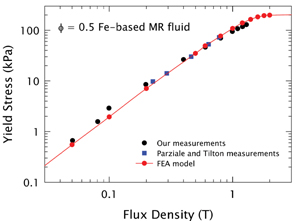Figure 2: Increase in shear yield stress with applied flux density in iron-based MR Fluids with volume fraction Ø=0.5 and comparison to a FEA magnetostatic model.

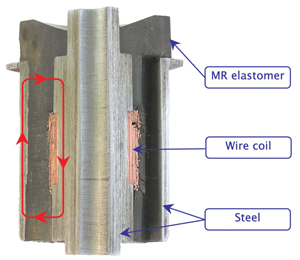Figure 3: Cross-section of a MR elastomer bushing, showing the wire coil that produces a magnetic field, the low-carbon steel magnetic circuit that delivers the field, and the MR elastomer material that responds to the field. The flux path is shown schematically in red.

The particles were assumed to be continuous, since each micrometer-sized particle can contain ~103 or more magnetic domains. Using symmetries appropriate to an isolated chain to reduce the problem size, we demonstrated that magnetic saturation controls the local fields and forces even in applied fields well below M_s/3 (M_s is the saturation magnetization of the particle and is roughly 1.7 x 10⁶ A/m for iron), the field at which isolated spherical particles saturate. The high relative permeability of the particles causes magnetic flux to be channeled into their polar regions, (Figure 1.) Because the material comprising the particle is magnetically nonlinear, the magnetization at the poles saturates at relatively low fields; the saturated zone grows in size as the field is increased, eventually engulfing the entire particle.

From these solutions and the Maxwell stress approach, we estimated the mechanical stress required to deform the chains by a given tilt or shear angle. We focused on the magnetically-controlled portion of the yield stress, defined as the maximum stress encountered as the shear angle is increased; the modeled yield stress compares quite favorably with measurements made on 50 volume percent MR fluids, (Figure 2.) The model reveals that the stress varies as B²—the behavior expected from a dipole model—only at very low fields. At applied fields sufficient to saturate the particle locally, the stress increases roughly as B^3/2, as confirmed by many experiments. The numerical model predicts a slight peak in the stress followed by a plateau signifying complete and uniform saturation of the particles. The maximum stress attainable at saturation varies as M_s².

Indeed, yield stresses of 100-200 kPa are routinely achieved in real MR materials, with a consistency of stiff putty. While they are much softer than most solids, MR fluids and magnetic powders are useful in a number of applications because the zero-field stresses they support are orders of magnitude smaller. Even higher stresses can be achieved by using particles with higher M_s, like iron-cobalt alloys. Other routes to high-stress materials include using a bimodal distribution of magnetizable particles, as implemented by Robert Foister and coworkers. One may regard the larger particles as embedded in a magnetic fluid comprising the smaller particles. Because the effective permeability of the suspending fluid is enhanced, the interparticle forces and resulting stresses increase.

Structure and Mechanics

The evolution and dynamics of the structures in MR materials have been of great interest. One key question is the response time required to form chains or agglomerates in quiescent conditions. Mark Jolly and coworkers used a magnetic induction technique to detect the formation of chains on time scales of the order of milliseconds. If the magnetic field can be introduced rapidly, the stresses generated by MR materials also appear on this time scale. Except in highly viscous host materials, the ubiquitous chains of particles eventually aggregate into multichain columns or stripes. Groups led by Alice Gast, Jing Liu, and others have used optical microscopy and light scattering to study the evolution of these chains in quiescent conditions. The aggregates typically grow in a power-law fashion with time. These observations are consistent with models of coarsening developed by Thomas Halsey and coworkers, in which lateral chain aggregation is driven by thermal fluctuations and chain defects. In sheared ER and MR fluids, large-scale oriented aggregates or "stripes" emerge over seconds or minutes, as observed by Frank Filisko, Georges Bossis, and others. Dan Klingenberg and coworkers have developed a continuum model of stripe formation that qualitatively predicts the geometry of these features and their dependence on shear rate.

The short range of the magnetic force dominates both the microscopic and macroscopic mechanics of magnetized MR materials, which act as brittle viscoelastic solids under dynamic mechanical loading, exhibiting mechanical nonlinearity even at very small strains ~10^-3. Rongjia Tao and coworkers have compressed magnetized MR fluids, enhancing the shear yield stress—reaching almost 1 MPa—perhaps by inducing both structural changes and enhanced frictional forces between particles.

Applications

MR fluids are ideally suited to applications in which damping force must be controlled rapidly and over a wide dynamic range. The first commercially available MR fluid linear damper was developed by Lord Corporation to improve vehicle seat dynamics for long-haul and off-road driving. Delphi's Magneride™, an automotive shock absorber, can be modulated electrically to control damping force on a several millisecond time scale necessary to improve vehicle ride. MR dampers have also been used to minimize vibrations in cable-stay bridges and to produce a more natural gait for amputees in above-the-knee prostheses. QED Technologies uses the magnetically tunable rheological properties of abrasive-doped magnetic dispersions to enable a computer- controlled optical polishing system.

MR fluids and magnetic powders are also used in torque-transfer clutches and brakes. Magnetic powder clutches controlled the torque transfer between the engine and the transmission on several 1950s-era minicars, and were also used to control main engine attitude on the Apollo Service Module in the 1960s. Potential automotive applications include clutches to control engine accessories like the air conditioner and cooling fan.

Magnetostriction in MR elastomers is manifest both in field-dependent length changes and viscoelastic moduli. Mark Nichols, myself, and coworkers explored automotive suspension bushings using these materials for controlling the ride and handling of automotive vehicles. Several groups have developed MR—elastomer-based tuned vibration absorbers—mass-spring systems—to absorb vibrations at mechanical frequencies that change over time. The mechanical non-linearity inherent in filled elastomers and exacerbated by the short-range magnetic interactions has so far prohibited successful commercial applications of these materials.

Applications of MR materials are enabled by a number of technologies, including additive chemistries to stabilize the suspended particles against irreversible settling or agglomeration, modify viscosity and lubricity, and inhibit oxidation and wear. Delivery and control of magnetic fields is obviously required in MR components; wire-coil electromagnets are often used. The design of an efficient magnetic circuit that does not add excess weight is essential. Required flux densities are of the order of 1 T—comparable to that utilized in most electric machines like motors. Control algorithms designed to minimize vibration amplitude have been developed for various MR devices and applications.

Opportunities

A few groups have used nanoparticles as a primary or secondary particulate in MR fluids. Nonetheless, the growing availability of nanoscale particulates has yet to be manifest in vastly improved MR materials; they may enable more stable, less abrasive MR fluids or MR elastomers with enhanced mechanical properties. Opportunities also exist to explore the effects of magnetic domain structure, which is particularly relevant as the particle size shrinks. The deformation and flow behavior of MR fluids and their coupling to applied field and other external factors has not been definitively modeled or explained. For example, little is known about instabilities in MR fluid flows. The behavior of MR fluids at short length scales, such as in microfluidic channels, has not been widely studied. While the past decade has seen much progress in understanding MR materials and in using them in commercial products, the field is still laden with opportunities and challenges for interested physicists.

John M. Ginder is the technical leader of the Physical and Environmental Sciences department of the Ford Motor Company.